Transforming the response

In general, transformations make interpretation harder.

We usually want to make statements about the response (not the transformed) response.

Predicted values are easily back-transformed, as well as the endpoints of confidence intervals.

Parameters often do not have nice interpretations on the backtransformed scale.

Special case: Log transformed response

Our fitted model on the transformed scale, predicts: \[ \hat{\log{y_i}} = \hat{\beta}_0 + \hat{\beta}_1x_{i1} + \ldots + \hat{\beta}_{p}x_{ip} \] If we backtransform, by taking exponential of both sides, \[ \hat{y_i} = \exp{\hat{\beta}_0}\exp{(\hat{\beta}_1x_{i1})}\ldots\exp{(\hat{\beta}_{p}x_{ip})} \]

So, an increase in \(x_1\) of one unit, will result in the predicted response being multiplied by \(exp(\beta_1)\).

If we are willing to assume that on the transformed scale the distribution of the response is symmetric, \[ \text{Median}({log(Y)}) = \E{log(Y)} = \beta_0 + \beta_1 x_1 + \ldots + \beta_{p}x_p \] and back-transforming gives, \[ \exp(\text{Median}({log(Y)})) = \text{Median}(Y) = \exp(\beta_0)\exp(\beta_1 x_1)\ldots\exp(\beta_{p}x_p) \]

So, an increase in \(x_1\) of one unit, will result in the median response being multiplied by \(exp(\beta_1)\).

(For monotone functions \(\text{Median}({f(Y)}) = f(\text{Median}(Y))\),

but \(\text{E}({f(Y)}) \ne f(E(Y))\) in general)

Example

library(faraway)
data(case0301, package = "Sleuth3")
head(case0301, 2)

##   Rainfall Treatment
## 1   1202.6  Unseeded
## 2    830.1  Unseeded

sumary(lm(log(Rainfall) ~ Treatment, data = case0301))

##                   Estimate Std. Error t value Pr(>|t|)
## (Intercept)        5.13419    0.31787 16.1519  < 2e-16
## TreatmentUnseeded -1.14378    0.44953 -2.5444  0.01408
## 
## n = 52, p = 2, Residual SE = 1.62082, R-Squared = 0.11

It is estimated the median rainfall for unseeded clouds is 0.32 times the median rainfall for seeded clouds.

(Assuming log rainfall is symmetric around its mean)

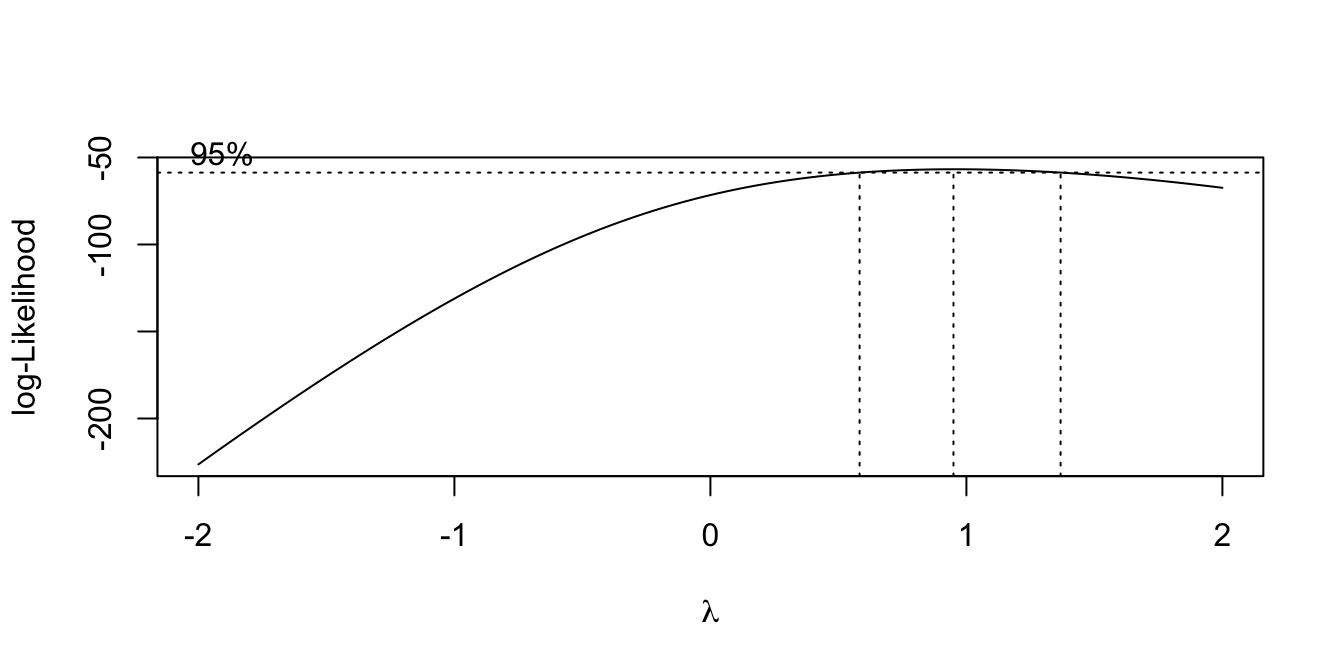
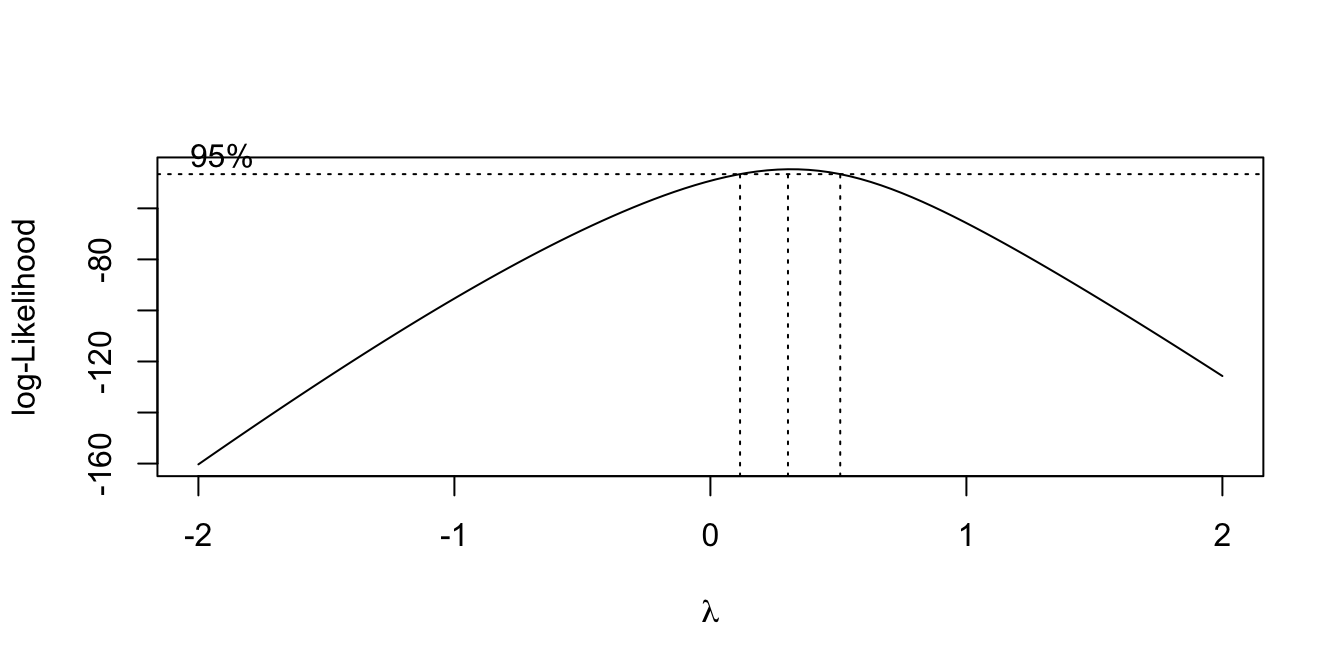
Box-Cox transformations

Assume, the response is positive, and \[ g(Y) = X\beta + \epsilon, \quad \epsilon \sim N(0, \sigma^2 I) \] and that \(g\) is of the form \[ g_{\lambda}(y) = \begin{cases} \frac{y^\lambda - 1}{\lambda} & \lambda \ne 0 \\ \log(y) & \lambda = 0 \end{cases} \]

Estimate \(\lambda\) with maximum likelihood.

For prediction, pick \(\lambda\) as the MLE.

For explanation, pick “nice” \(\lambda\) within 95% CI.

Example:

library(MASS)
data(savings, package = "faraway")
lmod <- lm(sr ~ pop15 + pop75 + dpi + ddpi, data = savings)
boxcox(lmod, plotit = TRUE)

Your turn:

data(gala, package = "faraway")
lmod <- lm(Species ~ Area + Elevation + Nearest + Scruz + Adjacent, 
  data = gala)
boxcox(lmod, plotit = TRUE)

Transforming the predictors

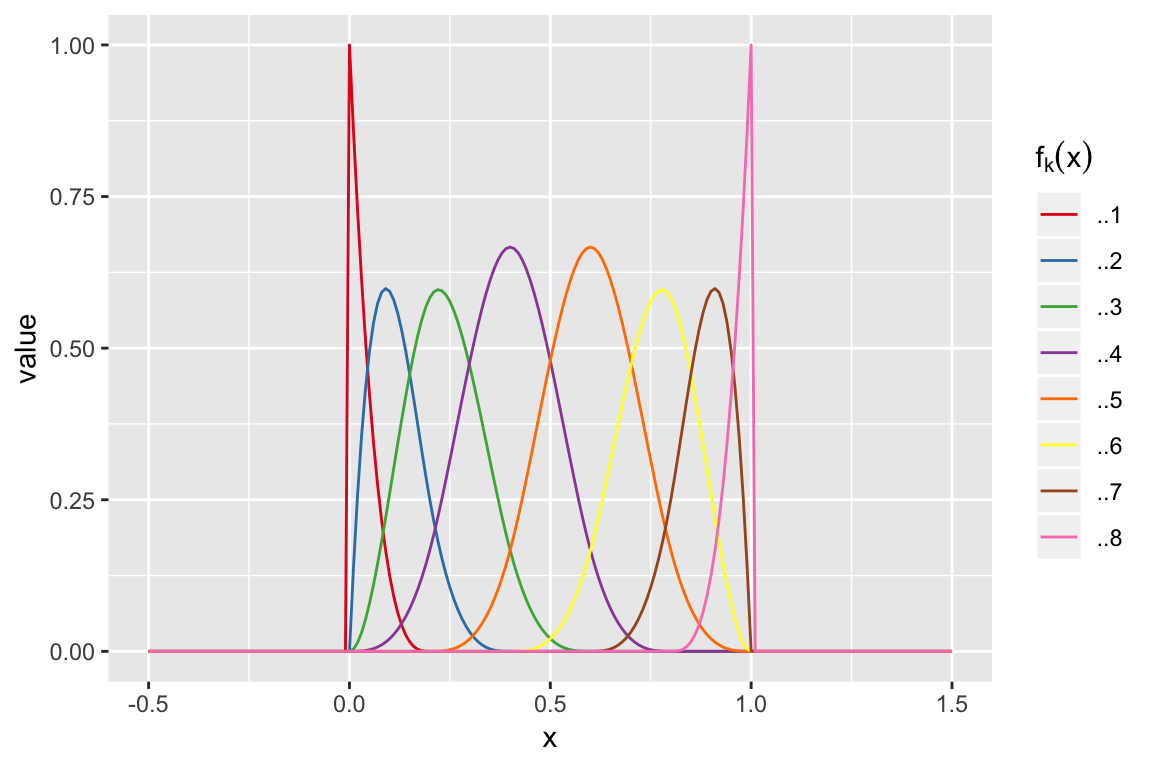
A very general approach is to let the function for each explanatory be represented by a finite set of basis functions. For example, for a single explanatory, X, \[ f(X) = \sum_{k = 1}^{K} \beta_k f_k(X) \] where \(f_k\) are the known basis functions, and \(\beta_k\) the unknown basis coefficients.

Then \[ \begin{aligned} y_i &= f(X_i) + \epsilon_i \\ y_i &= \beta_1 f_1(X_i) + \ldots + \beta_K f_K(X_i) + \epsilon_i \\ Y &= X'\beta + \epsilon \end{aligned} \] where the columns of \(X'\) are \(f_1(X)\), \(f_2(X)\) and we can find the \(\beta\) with the usual least squares approach.

Your turn:

What are the columns in the design matrix for the model:

\[ y_i = \beta_1 1\{X_i < 5\} + \beta_2 1\{X_i \ge 5\} + \beta_3 X_i 1\{X_i < 5\} + \beta_4 X_i 1\{X_i \ge 5\} + \epsilon_i \]

where \(X_i = i, i = 1, \ldots, 10\)?

What do the functions \(f_k(), k = 1, \ldots, 4\) look like?

Example: subset regression

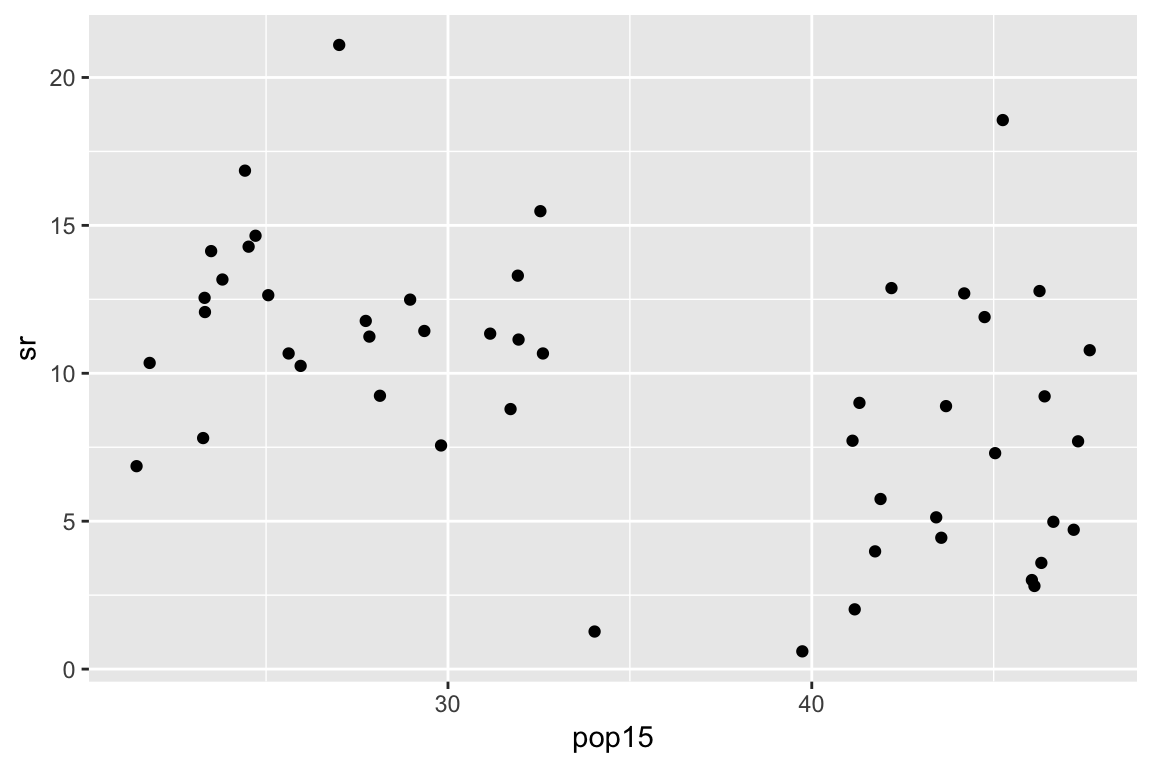
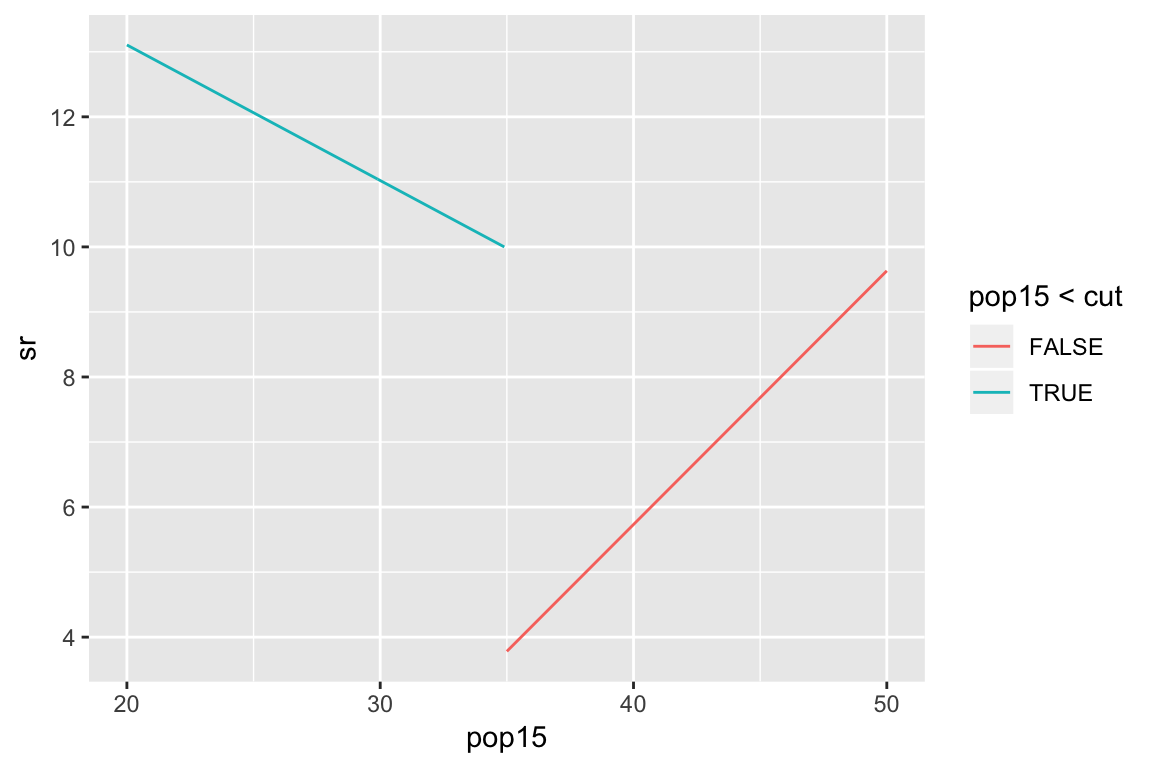
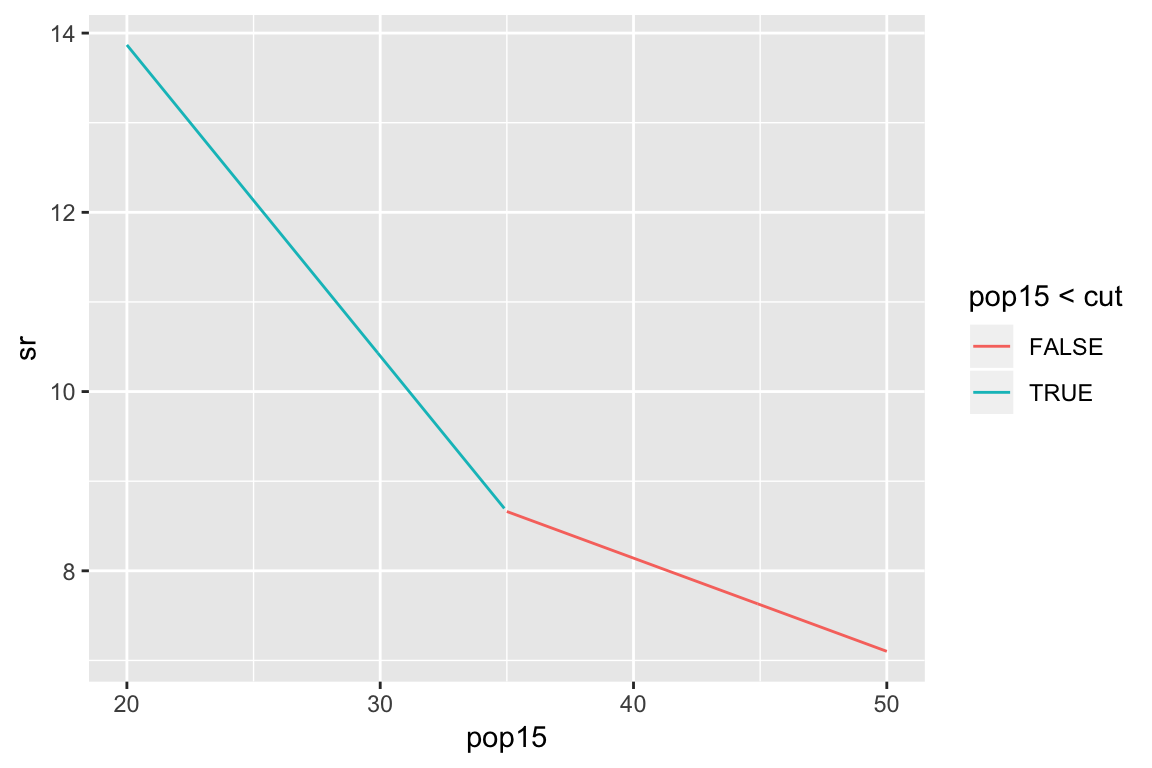
Example: subset regression

cut <- 35
X <- with(savings, cbind(
  as.numeric(pop15 < cut), 
  as.numeric(pop15 >= cut),
  pop15 * (pop15 < cut),
  pop15 * (pop15 >= cut)))

lmod <- lm(sr ~ X - 1, 
  data = savings)
summary(lmod)

Example: subset regression

Broken stick regression

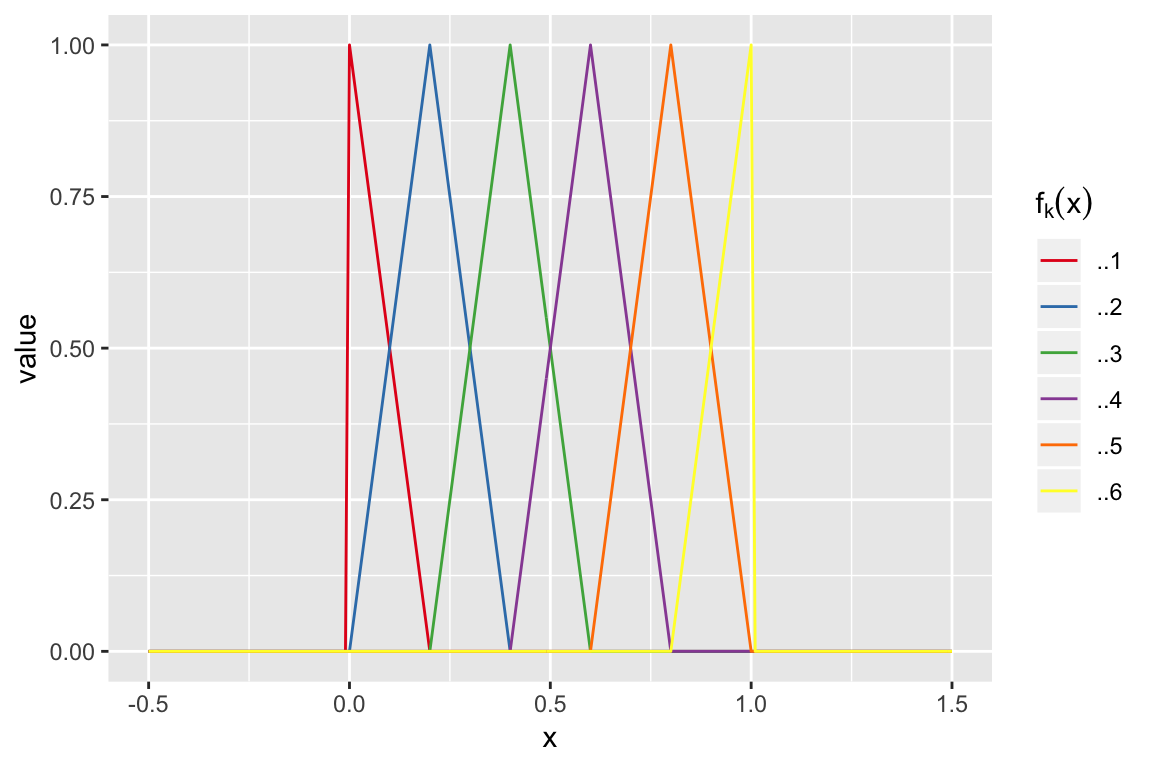
Broken stick:

\[ f_1(x) = \begin{cases} c - x & \text{if } x < c \\ 0 & \text{otherwise } \end{cases} \] \[ f_2(x) = \begin{cases} 0 & \text{if } x < c \\ x - c & \text{otherwise } \end{cases} \]

\[ y_i = \beta_0 + \beta_1 f_1(X_i) + \beta_2 f_2(X_i) + \epsilon_i \]

Example: broken stick regression

Polynomials

• Polynomials: \[ f_k(x) = x^k, \quad k = 1, \ldots, K \]

• Orthogonal polynomials

• Response surface, of degree \(d\) \[ f_{kl}(x, z) = x^{k}z^{l}, \quad k,l \ge 0 \text{ s.t. } k + l = d \]

Cubic Splines

Knots: 0, 0, 0, 0, 0.2, 0.4, 0.6, 0.8, 1, 1, 1 and 1

Linear splines

Knots: 0, 0, 0.2, 0.4, 0.6, 0.8, 1 and 1

In practice splines provide a flexible fit

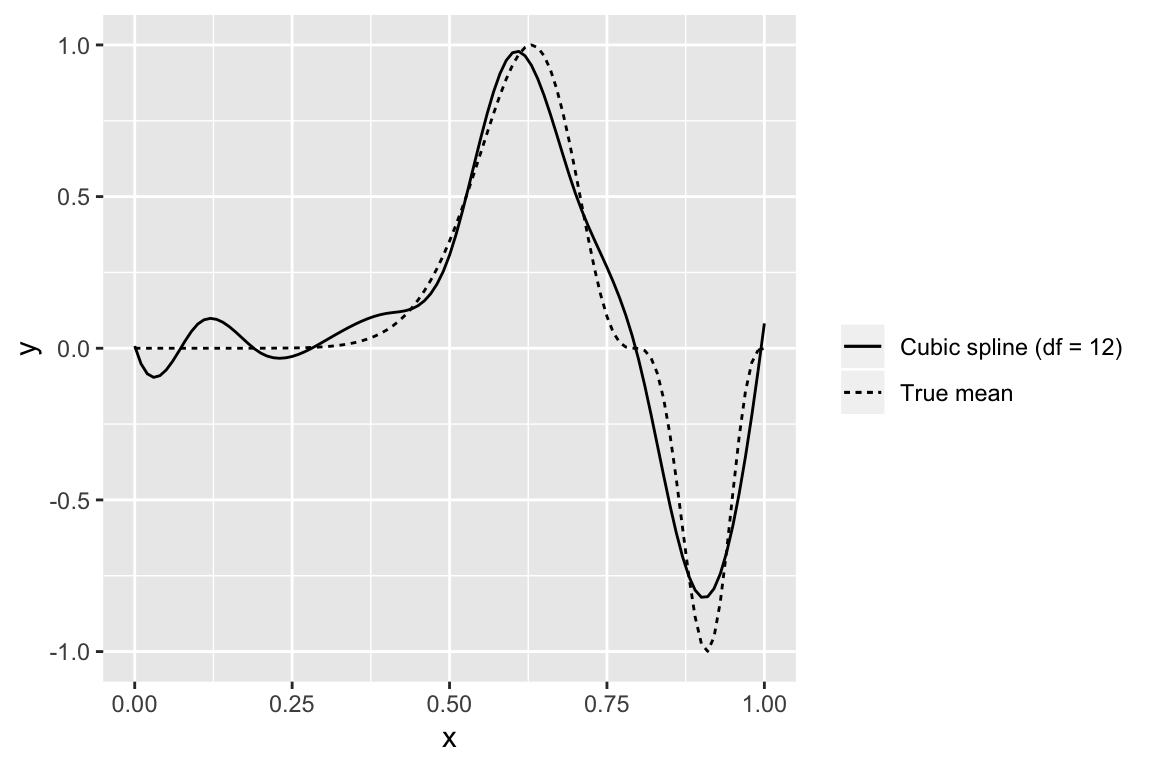
• Smoothing splines: have a large set of basis functions, but penalize against wiggliness

• Generalized Additive Models: simultaneously estimate

\[ y_i = f(x_{i1}) + g(x_{i2}) + \ldots + \epsilon_i \]

Transforming predictors with basis functions

• The parameters in these regressions no longer have nice interpretations. The best way to present the results is a plot of the estimated function for each X, (or surfaces if variables interact),

• The significance of a variable can still be assessed with an Extra Sum of Squares F-test, comparing to a model without any of the terms relating to a particular variable.