Today
Problems with the errors
- Generalized Least Squares
- Lack of fit F-tests
- Robust regression
Generalized Least Squares
\[ Y = X\beta + \epsilon \]
We have assumed \(\Var{\epsilon} = \sigma^2 I\), but what if we know \(\Var{\epsilon} = \sigma^2 \Sigma\), where \(\sigma^2\) is unknown, but \(\Sigma\) is known. For example, we know the form of the correlation and/or non-constant variance in the response.
The usual least squares estimates \(\hat{\beta}_{LS}\) are unbiased, but they are no longer BLUE.
Let \(S\) be the matrix square root of \(\Sigma\), i.e. \(\Sigma = SS^T\).
Define a new regression equation by multiplying both sides by \(S^{-1}\): \[ \begin{aligned} S^{-1}Y &= S^{-1}X\beta + S^{-1}\epsilon \\ Y' &= X' \beta + \epsilon' \end{aligned} \]
Your Turn
Show \(\Var{\epsilon'} = \Var{S^{-1}\epsilon} = \sigma^2 I\).
Show the least squares estimates for the new regression equation reduce to: \[ \hat{\beta} = (X^T\Sigma^{-1} X)^{-1}X^T\Sigma^{-1} Y \]
Can also show \(\Var{\beta} = (X^T\Sigma^{-1} X)^{-1} \sigma^2\).
The estimates: \(\hat{\beta} = (X^T\Sigma^{-1} X)^{-1}X^T\Sigma^{-1} Y\) are known as estimates.
In practice, \(\Sigma\) might only be know up to a few parameters that also need to be estimated.
Common cases of GLS
- \(\Sigma\) defines a temporal or spatial correlation structure
- \(\Sigma\) defines a grouping structure
- \(\Sigma\) is diagonal and defines a weighting structure ()
In R
?lm # use weights argument
library(nlme)
?gls # has weights and/or correlation argumentOat yields
Data from an experiment to compare 8 varieties of oats. The growing area was heterogeneous and so was grouped into 5 blocks. Each variety was sown once within each block and the yield in grams per 16ft row was recorded.
\[ \text{yield}_i = \beta_0 + \beta_1 \text{variety}_i + \epsilon_i \quad i=1, \ldots, 40 \] \[ \Var{\epsilon_i} = \sigma^2, \quad \text{Cor}(\epsilon_i, \epsilon_j) = \begin{cases} \rho, & \text{block}_i = \text{if block}_j \\ 0, & \text{otherwise} \end{cases} \]
library(nlme)
fit_gls <- gls(yield ~ variety, data = oatvar,
correlation = corCompSymm(form = ~ 1 | block))Oat yields in R
intervals(fit_gls)## Approximate 95% confidence intervals
##
## Coefficients:
## lower est. upper
## (Intercept) 291.542999 334.4 377.2570009
## variety2 -4.903898 42.2 89.3038984
## variety3 -18.903898 28.2 75.3038984
## variety4 -94.703898 -47.6 -0.4961016
## variety5 57.896102 105.0 152.1038984
## variety6 -50.903898 -3.8 43.3038984
## variety7 -63.103898 -16.0 31.1038984
## variety8 2.696102 49.8 96.9038984
## attr(,"label")
## [1] "Coefficients:"
##
## Correlation structure:
## lower est. upper
## Rho 0.06596382 0.3959955 0.7493731
## attr(,"label")
## [1] "Correlation structure:"
##
## Residual standard error:
## lower est. upper
## 33.39319 47.04679 66.28298Lack of fit F-tests
\(\hat{\sigma^2}\) should be (if our model is specified correctly) an unbiased estimate of \(\sigma^2\).
A “model free” estimate of \(\sigma^2\) is available if there are replicates (multiple observations at combinations of the explanatory values).
If our \(\hat{\sigma^2}\) from our model is much bigger than the “model-free” estimate, we have evidence of .
In practice
Fit a saturated model. Compare saturated model to proposed model with an F-test. .
Saturated: every combination of explanatory variables is allowed its own mean (i.e. every group of replicates is allowed its own mean). A model that includes every explantory as categorical and every possible interaction between variables.
Example
data(corrosion, package = "faraway")
lm_cor <- lm(loss ~ Fe, data = corrosion)
lm_sat <- lm(loss ~ factor(Fe), data = corrosion)
anova(lm_cor, lm_sat)## Analysis of Variance Table
##
## Model 1: loss ~ Fe
## Model 2: loss ~ factor(Fe)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 11 102.850
## 2 6 11.782 5 91.069 9.2756 0.008623 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# significant lack of fit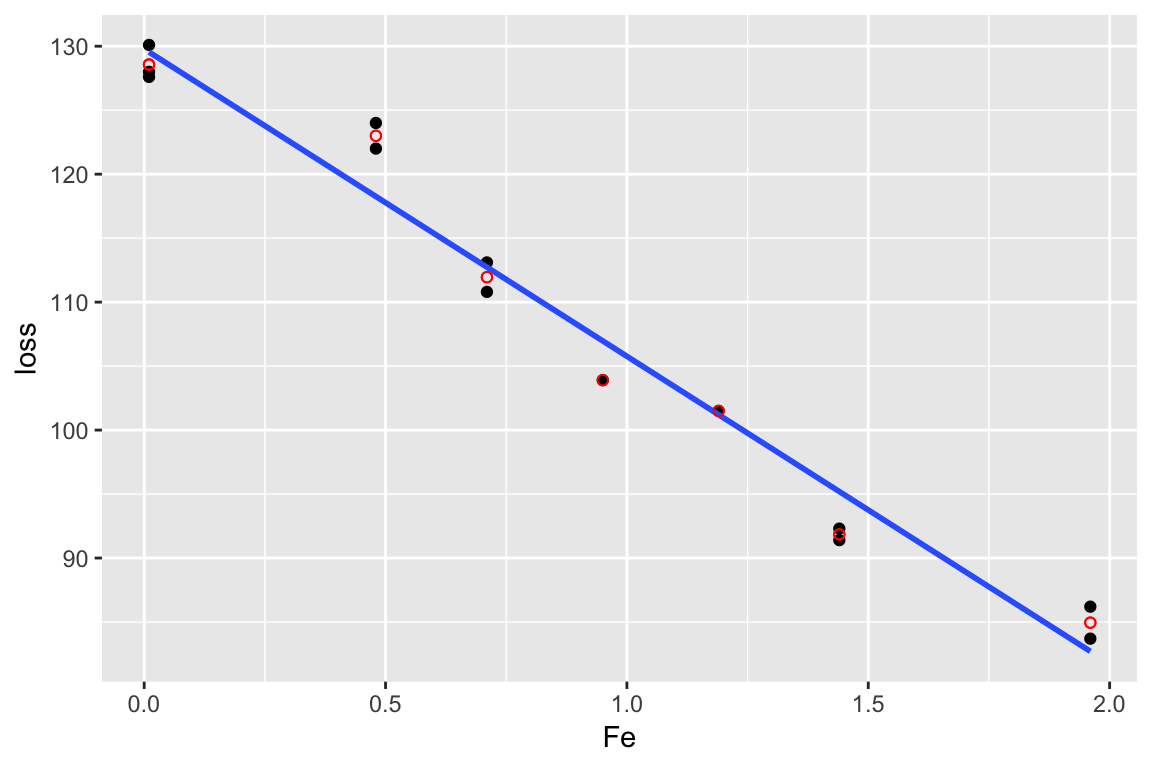
Robust regression
Remember to define our least squares estimates we looked for \(\beta\) to minimise \[ \sum_{i=1}^n \left(y_i - x_i^T\beta \right)^2 \]
In practice, since we are squaring residuals, observations with large residuals carry a lot of weight. For, robust regression, we want to downweight the observations with large residuals.
The idea of M-estimators is to extend this to the general situation where we want to find \(\beta\) to minimise \[ \sum_{i=1}^n \rho(y_i - x_i^T\beta) \] where \(\rho()\) is some function we specify.
\[ \sum_{i=1}^n \rho(y_i - x_i^T\beta) \]
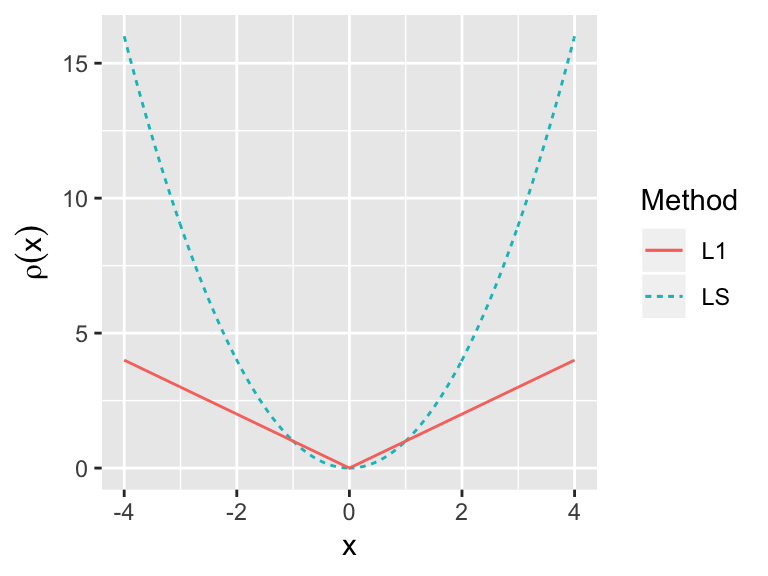
- Least squares: \(\rho(e_i) = e_i^2\)
- Least absolute deviation, L\(_1\) regression: \(\rho(e_i) = |e_i|\)
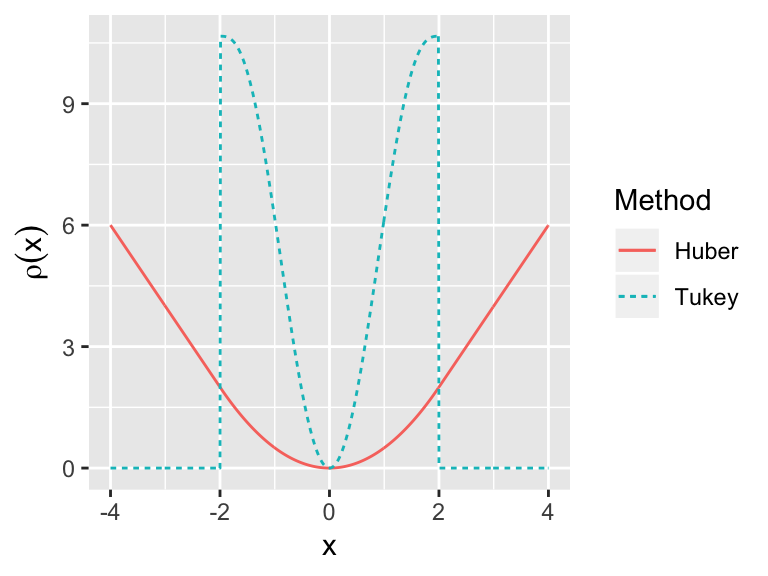
- Huber’s method \[ \rho(e_i) = \begin{cases} e_i^2/2 & \text{if } |e_i| \le c\\ c|e_i| - c^2/2 & \text{otherwise} \end{cases} \]
- Tukey’s bisquare \[ \rho(e_i) =\begin{cases} \frac{1}{6}(c^6 - (c^2 - e_i^2)^3) & |e_i| \le c\\ 0 & \text{otherwise} \end{cases} \]
The models are usually fit in an iterative process.
Least trimmed squares
Minimise the smallest residuals \[ \sum_{i=1}^q e_{(i)}^2 \] where \(q\) is some number smaller than \(n\) and \(e_{(i)}\) is the ith smallest residual.
One choice, \(q=\lfloor n/2 \rfloor + \lfloor (p+1)/2 \rfloor\)
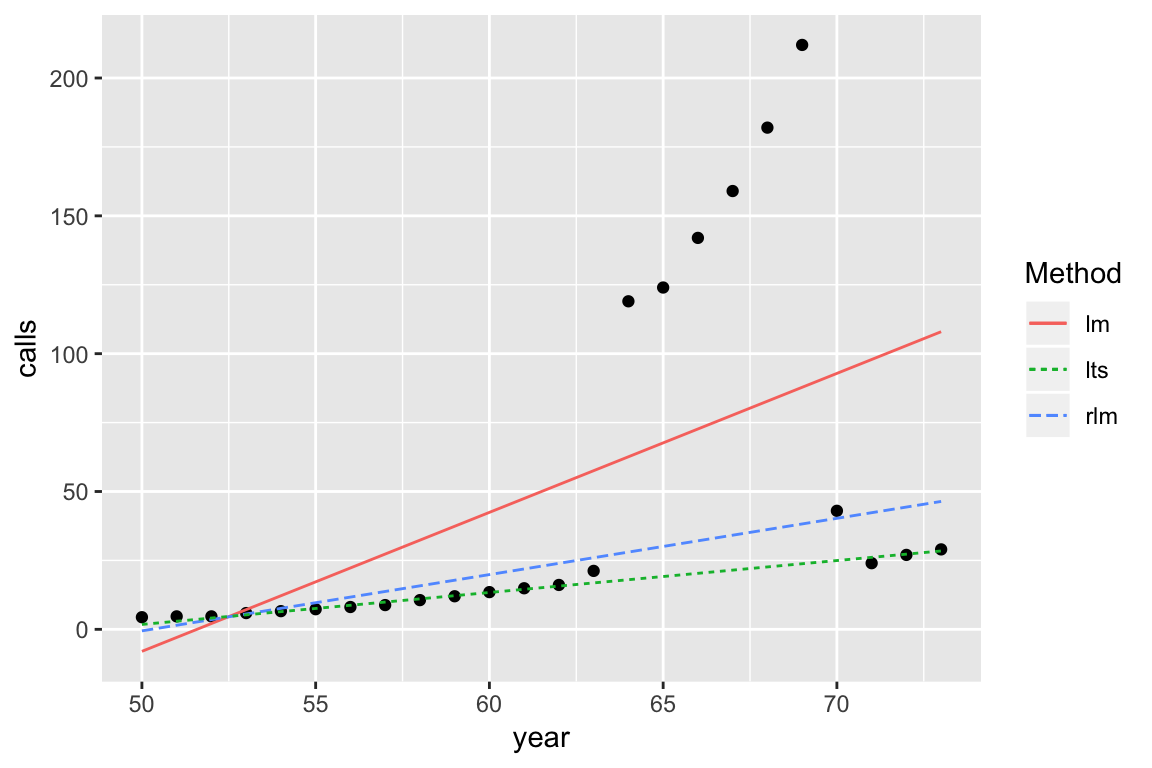
Annual numbers of telephone calls in Belgium