Inference in regression: confidence intervals Jan 28 2019

Today

Last time…

Certain hypotheses of interest can be set up as competing models. A full model and a simpler model (nested in the full model). A.K.A testing models.

Identify the models of interest. Fit both. Check fit of full model. Find F-statistic, and answer questions of interest.

Another way to set up F-tests A.K.A testing linear parametric functions

Assuming the regression model: \[ Y = X\beta + \epsilon, \quad \epsilon \sim N(0, \sigma^2 I) \] Consider the hypotheses: \[ \begin{aligned} H_0: K^T \beta = m \\ H_1: K^T \beta \ne m \end{aligned} \] where \(K_{k \times p}\) matrix with rank(K) = k.

Then under the null hypothesis, \[ F = \frac{\left((K^T\beta - m)^T \left(K^T(X^TX)^{-1}K \right)^{-1} (K^T\beta - m)\right)/k}{\text{RSS}/(n-p)} \sim F_{k, n-p} \]

(Don’t memorise for ST552, maybe for comps)

You get the same answer

This alternative is equivalent to the model testing setup we considered. Every null hypothesis of the form \(K^T \beta = m\) is comparing a full and reduced model and vice versa.

For example, consider \[ K = \left(\begin{matrix} 0 \\ \vdots \\ 0 \\ 1\\ 0 \\ \vdots \\ 0 \end{matrix}\right), \quad m = 0 \hspace{3cm} \] where the 1 in \(K\) occurs in the \(i\)th row.

What is the null hypothesis being tested?

Your turn

What are \(K\) and \(m\) for exercises 1 and 5 from the handout from last time? HW#4

Confidence intervals for individual \(\beta_j\)

The t-test for an individual parameter can be flipped around to give \(100(1 - \alpha)\%\) confidence intervals of the form

\[ \hat{\beta_j} \pm t^{(\alpha/2)}_{n-p} \SE{\hat{\beta_j}} \]

(Remember \(\SE{\hat{\beta_j}}\) is coming from the diagonal entry of the estimated variance-covariance matrix.)

Coagulation times

Dataset comes from a study of blood coagulation times. 24 animals were randomly assigned to four different diets and the samples were taken in a random order.

Consider the model: \[ \begin{aligned} \text{Coagulation time (s)}_i &= \beta_0 + \beta_1 1\{\text{Diet B}\}_i \\ &+ \beta_2 1\{\text{Diet C}\}_i + \beta_3 1\{\text{Diet D}\}_i + \epsilon_i \end{aligned} \]

Coagulation

data(coagulation, package = "faraway")
ggplot(coagulation, aes(diet, coag)) +
  geom_dotplot(binaxis = "y",  binwidth = 1)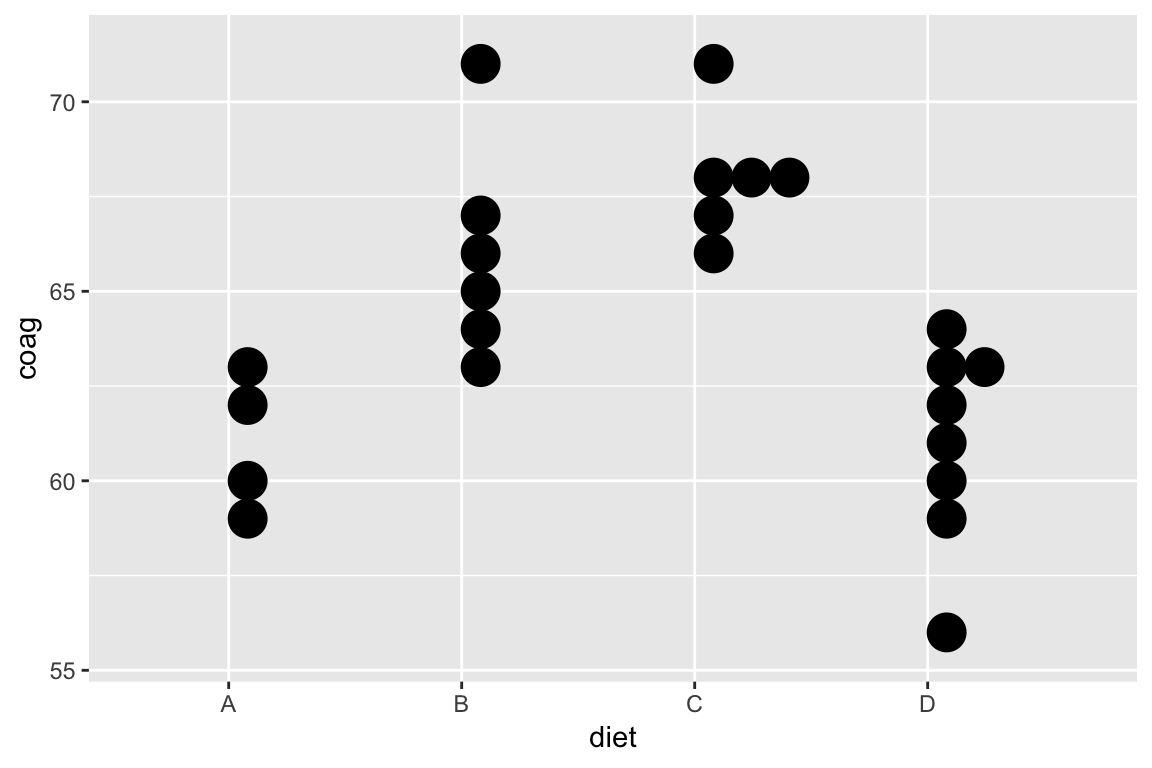

Your turn: cont.

fit <- lm(coag ~ diet, data = coagulation)
broom::tidy(fit) %>%  
  knitr::kable(digits = 2)
term estimate std.error statistic p.value
(Intercept) 61 1.18 51.55 0
dietB 5 1.53 3.27 0
dietC 7 1.53 4.58 0
dietD 0 1.45 0.00 1

Find a 95% CI for \(\beta_0\)?

\(t_{n-p}^{(0.975)}= t_{20}^{(0.975)} = 2.09\)

Your turn: cont.

In R:

broom::tidy(fit, conf.int = TRUE)
# OR
(cis <- confint(fit))

Confidence intervals for linear combinations of parameters of \(\beta_j\)

Similarly, confidence intervals for a linear combination of the parameters, \(c^T\beta\) where \(c_{p\times 1}\), can be formed with \[ c^T\hat{\beta} \pm t^{(\alpha/2)}_{n-p} \sqrt{\hat{\sigma}^2 c^T(X^TX)^{-1}c} \]

Your turn

With the coagulation example \[ \begin{aligned} \text{Coagulation time (s)}_i &= \beta_0 + \beta_1 1\{\text{Diet B}\}_i \\ &+ \beta_2 1\{\text{Diet C}\}_i + \beta_3 1\{\text{Diet D}\}_i + \epsilon_i \end{aligned} \]

What is \(c\) for the linear combination \(\beta_0 - \beta_1\)?

Find \(c^T(X^TX)^{-1}c\).

X <- model.matrix(fit)
round(solve(t(X) %*% X), 2)
##             (Intercept) dietB dietC dietD
## (Intercept)        0.25 -0.25 -0.25 -0.25
## dietB             -0.25  0.42  0.25  0.25
## dietC             -0.25  0.25  0.42  0.25
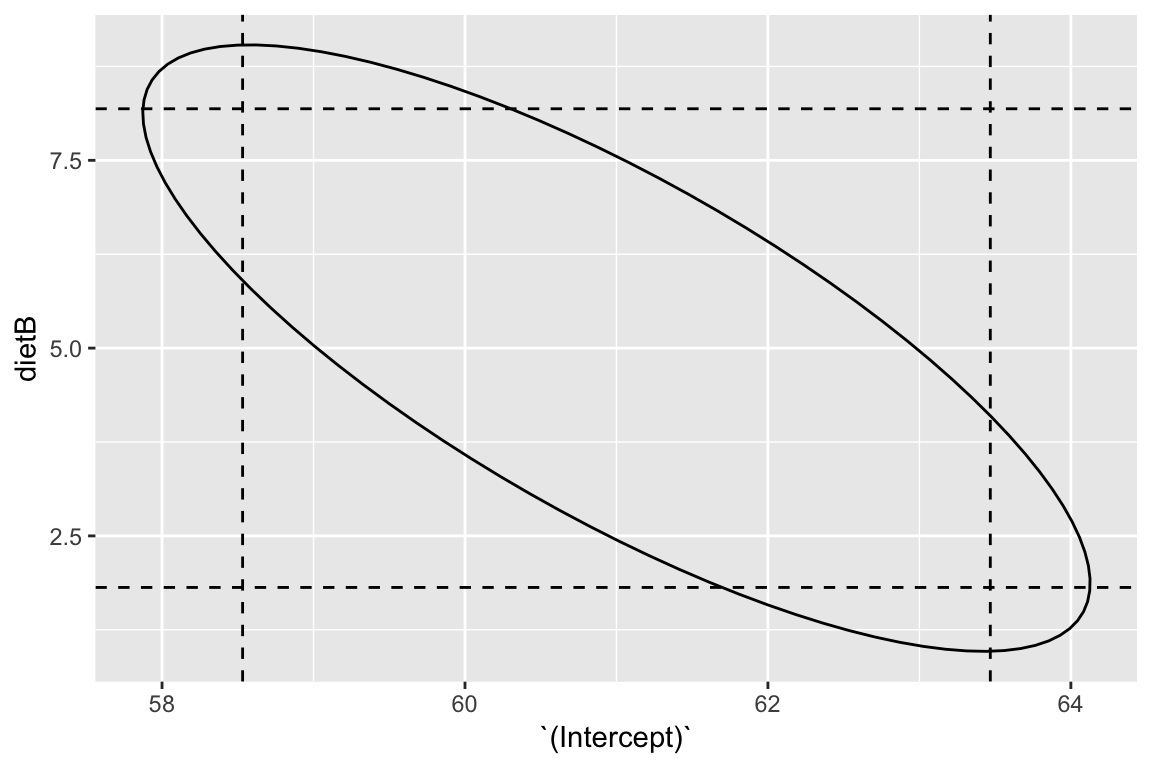
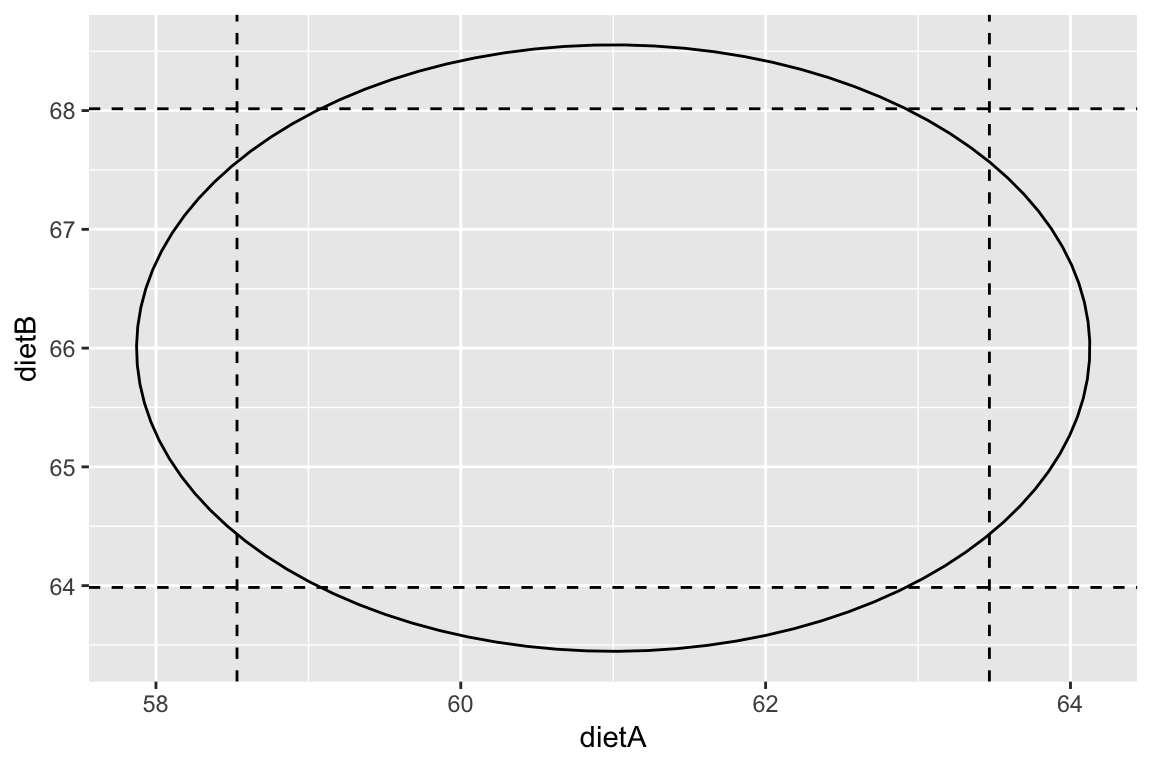
## dietD             -0.25  0.25  0.25  0.37

Joint confidence regions

A joint \(100(1-\alpha)\%\) confidence for the vector \(\beta\) can be formed using, \[ (\hat{\beta} - \beta)^TX^TX(\hat{\beta} - \beta) \le p \hat{\sigma}^2 F^{(\alpha)}_{p, n-p} \] and results in \(p\)-dimensional ellipsoids (very hard to visualise, but essential for communicating joint uncertainty when the parameters are correlated).

2D ellipsoid example: correlated estimates

For example, \((\beta_0, \beta_1)\) in

\[ \begin{aligned} \text{Coagulation time (s)}_i &= \beta_0 + \beta_1 1\{\text{Diet B}\}_i \\ &+ \beta_2 1\{\text{Diet C}\}_i + \beta_3 1\{\text{Diet D}\}_i + \epsilon_i \end{aligned} \]

2D ellipsoid example: uncorrelated estimates

Compare to \(\gamma_0\) and \(\gamma_1\) in this parameterization: \[ \begin{aligned} \text{Coagulation time (s)}_i &= \gamma_0 1\{\text{Diet A}\}_i + \gamma_1 1\{\text{Diet B}\}_i \\ &+ \gamma_2 1\{\text{Diet C}\}_i + \gamma_3 1\{\text{Diet D}\}_i + \epsilon_i \end{aligned} \] 

fit_nointercept <- lm(coag ~ diet - 1, data = coagulation)